How To Add To Sets In Python

A set up is an unordered collection of items. Every fix element is unique (no duplicates) and must exist immutable (cannot exist inverse).

Yet, a set itself is mutable. We can add or remove items from it.

Sets tin also be used to perform mathematical set operations like matrimony, intersection, symmetric departure, etc.

Creating Python Sets

A set is created by placing all the items (elements) inside curly braces {}, separated by comma, or by using the built-in prepare() function.

It tin accept any number of items and they may exist of different types (integer, float, tuple, string etc.). Simply a set cannot have mutable elements similar lists, sets or dictionaries as its elements.

          # Different types of sets in Python # fix of integers my_set = {1, 2, three} print(my_set)  # fix of mixed datatypes my_set = {ane.0, "Hullo", (1, 2, three)} print(my_set)

Output

          {1, 2, 3} {1.0, (1, ii, 3), 'Hello'}

Try the post-obit examples likewise.

          # set cannot accept duplicates # Output: {1, ii, 3, four} my_set = {1, two, three, 4, 3, 2} impress(my_set)  # we can make set from a list # Output: {i, 2, three} my_set = gear up([1, 2, 3, two]) impress(my_set)  # set cannot have mutable items # here [3, four] is a mutable list # this will cause an fault.  my_set = {i, 2, [3, 4]}

Output

          {1, 2, 3, iv} {1, 2, 3} Traceback (most recent phone call last):   File "<string>", line 15, in <module>     my_set = {i, ii, [3, 4]} TypeError: unhashable type: 'list'

Creating an empty set up is a flake tricky.

Empty curly braces {} will make an empty dictionary in Python. To make a fix without any elements, nosotros apply the set() function without any statement.

          # Distinguish prepare and dictionary while creating empty set  # initialize a with {} a = {}  # cheque data type of a print(type(a))  # initialize a with set() a = set()  # check data type of a impress(type(a))

Output

          <class 'dict'> <form 'ready'>

Modifying a set in Python

Sets are mutable. All the same, since they are unordered, indexing has no meaning.

We cannot access or change an element of a prepare using indexing or slicing. Set data type does not support it.

We can add a single element using the add() method, and multiple elements using the update() method. The update() method can take tuples, lists, strings or other sets every bit its argument. In all cases, duplicates are avoided.

          # initialize my_set my_set = {ane, 3} print(my_set)  # my_set[0] # if you uncomment the above line # yous will go an error # TypeError: 'set' object does not support indexing  # add an element # Output: {i, ii, 3} my_set.add(2) impress(my_set)  # add together multiple elements # Output: {1, 2, iii, four} my_set.update([2, 3, 4]) print(my_set)  # add together listing and fix # Output: {1, 2, three, iv, v, 6, viii} my_set.update([4, 5], {one, 6, viii}) impress(my_set)

Output

          {1, 3} {i, 2, 3} {ane, 2, 3, 4} {1, ii, 3, 4, 5, 6, 8}

Removing elements from a fix

A particular particular can be removed from a set using the methods discard() and remove().

The only difference betwixt the two is that the discard() part leaves a prepare unchanged if the element is not present in the set. On the other manus, the remove() function will heighten an mistake in such a condition (if element is non present in the ready).

The following example volition illustrate this.

          # Difference betwixt discard() and remove()  # initialize my_set my_set = {1, three, four, five, 6} print(my_set)  # discard an chemical element # Output: {1, iii, 5, vi} my_set.discard(4) print(my_set)  # remove an element # Output: {ane, 3, 5} my_set.remove(6) print(my_set)  # discard an element # not nowadays in my_set # Output: {1, 3, v} my_set.discard(ii) print(my_set)  # remove an element # not nowadays in my_set # you will get an error. # Output: KeyError  my_set.remove(2)

Output

          {one, 3, 4, 5, 6} {1, three, 5, half-dozen} {1, 3, 5} {1, 3, v} Traceback (nearly recent call last):   File "<string>", line 28, in <module> KeyError: 2

Similarly, nosotros can remove and render an detail using the pop() method.

Since set up is an unordered data type, there is no way of determining which item will be popped. Information technology is completely arbitrary.

We can likewise remove all the items from a set up using the articulate() method.

          # initialize my_set # Output: fix of unique elements my_set = set("HelloWorld") print(my_set)  # pop an element # Output: random element print(my_set.pop())  # pop another element my_set.popular() print(my_set)  # articulate my_set # Output: set() my_set.clear() print(my_set)

Output

          {'H', 'l', 'r', 'W', 'o', 'd', 'e'} H {'r', 'W', 'o', 'd', 'east'} set()

Python Set Operations

Sets can exist used to conduct out mathematical set operations similar union, intersection, difference and symmetric departure. We tin do this with operators or methods.

Let us consider the following two sets for the following operations.

          >>> A = {1, 2, iii, 4, five} >>> B = {iv, 5, half dozen, seven, eight}

Ready Spousal relationship

Set Union in Python — Ready Union in Python

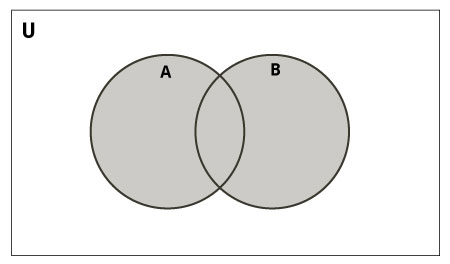
Matrimony of A and B is a set of all elements from both sets.

Union is performed using | operator. Same can exist accomplished using the spousal relationship() method.

          # Set union method # initialize A and B A = {1, 2, 3, 4, v} B = {4, 5, 6, seven, viii}  # utilize | operator # Output: {1, 2, 3, iv, five, 6, 7, viii} print(A | B)

Output

          {ane, 2, 3, 4, 5, 6, vii, 8}

Try the post-obit examples on Python crush.

          # use marriage function >>> A.union(B) {one, 2, 3, iv, 5, 6, vii, 8}  # employ matrimony function on B >>> B.union(A) {1, 2, three, four, 5, half-dozen, seven, 8}

Fix Intersection

Set Intersection in Python — Fix Intersection in Python

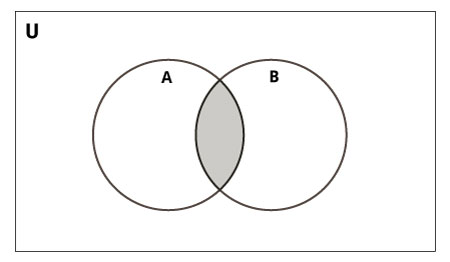
Intersection of A and B is a fix of elements that are common in both the sets.

Intersection is performed using & operator. Same can exist accomplished using the intersection() method.

          # Intersection of sets # initialize A and B A = {1, two, 3, 4, five} B = {4, 5, half-dozen, seven, 8}  # use & operator # Output: {iv, v} impress(A & B)

Output

          {4, 5}

Attempt the following examples on Python shell.

          # utilize intersection role on A >>> A.intersection(B) {4, 5}  # use intersection office on B >>> B.intersection(A) {four, 5}

Set Difference

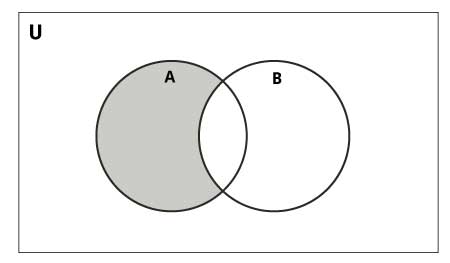
Difference of the set B from set A(A - B) is a set of elements that are only in A just non in B. Similarly, B - A is a set up of elements in B but not in A.

Departure is performed using - operator. Aforementioned tin exist accomplished using the difference() method.

          # Difference of 2 sets # initialize A and B A = {i, ii, 3, 4, 5} B = {4, five, 6, seven, 8}  # use - operator on A # Output: {1, 2, 3} print(A - B)

Output

          {1, 2, 3}

Try the following examples on Python trounce.

          # use difference function on A >>> A.difference(B) {1, 2, 3}  # utilize - operator on B >>> B - A {8, 6, 7}  # use deviation part on B >>> B.deviation(A) {8, 6, 7}

Set Symmetric Deviation

Set Symmetric Difference in Python — Fix Symmetric Difference in Python

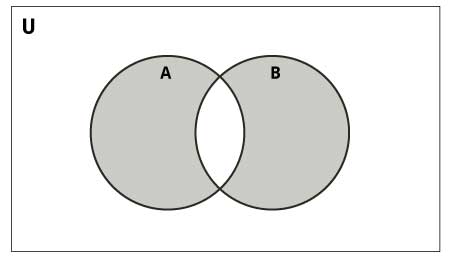
Symmetric Difference of A and B is a set of elements in A and B simply not in both (excluding the intersection).

Symmetric difference is performed using ^ operator. Same can exist accomplished using the method symmetric_difference().

          # Symmetric difference of ii sets # initialize A and B A = {one, ii, 3, iv, 5} B = {4, 5, 6, 7, 8}  # utilize ^ operator # Output: {1, 2, three, 6, vii, 8} impress(A ^ B)

Output

          {one, 2, 3, half-dozen, 7, viii}

Try the following examples on Python shell.

          # use symmetric_difference office on A >>> A.symmetric_difference(B) {one, 2, iii, 6, 7, 8}  # use symmetric_difference part on B >>> B.symmetric_difference(A) {i, 2, 3, 6, 7, eight}

Method	Description
add()	Adds an element to the fix
clear()	Removes all elements from the set
copy()	Returns a copy of the set
deviation()	Returns the departure of 2 or more than sets as a new set
difference_update()	Removes all elements of another set from this set
discard()	Removes an chemical element from the set if information technology is a member. (Do aught if the element is not in fix)
intersection()	Returns the intersection of two sets as a new set
intersection_update()	Updates the set with the intersection of itself and another
isdisjoint()	Returns `True` if two sets have a null intersection
issubset()	Returns `Truthful` if another set up contains this gear up
issuperset()	Returns `Truthful` if this set contains another set
popular()	Removes and returns an arbitrary set element. Raises `KeyError` if the set is empty
remove()	Removes an element from the set. If the element is not a member, raises a `KeyError`
symmetric_difference()	Returns the symmetric divergence of two sets every bit a new set
symmetric_difference_update()	Updates a set up with the symmetric difference of itself and some other
union()	Returns the union of sets in a new set
update()	Updates the set with the union of itself and others

Other Set Operations

Set Membership Test

We can test if an particular exists in a set or non, using the in keyword.

          # in keyword in a set # initialize my_set my_set = set("apple")  # check if 'a' is present # Output: Truthful impress('a' in my_set)  # check if 'p' is present # Output: Faux print('p' non in my_set)

Output

          Truthful Faux

Iterating Through a Ready

We tin iterate through each item in a set using a for loop.

          >>> for letter in set up("apple tree"): ...     print(letter) ...     a p e l

Built-in Functions with Set

Congenital-in functions like all(), whatever(), enumerate(), len(), max(), min(), sorted(), sum() etc. are ordinarily used with sets to perform unlike tasks.

Function	Description
all()	Returns `True` if all elements of the set are true (or if the fix is empty).
any()	Returns `Truthful` if whatsoever element of the gear up is true. If the set up is empty, returns `False`.
enumerate()	Returns an enumerate object. It contains the alphabetize and value for all the items of the set equally a pair.
len()	Returns the length (the number of items) in the set.
max()	Returns the largest item in the set.
min()	Returns the smallest detail in the set.
sorted()	Returns a new sorted listing from elements in the ready(does non sort the set itself).
sum()	Returns the sum of all elements in the set.

Python Frozenset

Frozenset is a new class that has the characteristics of a set, only its elements cannot be changed once assigned. While tuples are immutable lists, frozensets are immutable sets.

Sets beingness mutable are unhashable, and then they can't exist used every bit dictionary keys. On the other paw, frozensets are hashable and can exist used as keys to a dictionary.

Frozensets can be created using the frozenset() function.

This data type supports methods similar re-create(), difference(), intersection(), isdisjoint(), issubset(), issuperset(), symmetric_difference() and union(). Existence immutable, it does non have methods that add or remove elements.

          # Frozensets # initialize A and B A = frozenset([1, 2, iii, 4]) B = frozenset([3, 4, 5, 6])

Effort these examples on Python shell.

          >>> A.isdisjoint(B) False >>> A.difference(B) frozenset({1, 2}) >>> A | B frozenset({one, 2, 3, 4, 5, half-dozen}) >>> A.add(3) ... AttributeError: 'frozenset' object has no attribute 'add'